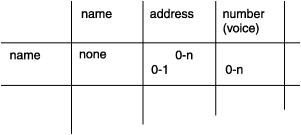
图: 反映个人电话号码簿实体的矩阵

您可以忽略此矩阵的阴影部分。您必须考虑对角单元格;即,您必须询问“A 与另一个 A 之间存在什么关系?”这个问题。在此模型中,答案始终是“none”。在不同的 name 之间或者不同的 address 之间不存在关系,至少您不需要在此模型中记录任何关系。当 A 与另一个 A 之间存在关系时,表示找到了递归关系。(请参阅解析其他特殊关系。)
图: 包含初始关系的矩阵
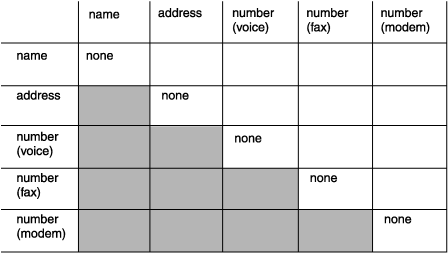
尽管在此模型中没有实体与它们本身相关,但在其他模型中情况并非总是如此。典型的示例是:一个雇员是另一个雇员的经理。另一个示例出现在制造业:一个部件实体是另一个部件的组件。
- 一对一 (1:1),在此关系中,对于一个实体 B,存在至多一个实体 A,并且对于一个 A,也是存在至多一个 B。
- 一对多 (1:n),在此关系中,绝不会存在多个实体 A,但可以有若干个实体 B 与 A 相关(反之亦然)。
- 多对多 (m:n),在此关系中,可以有若干个实体 A 与一个 B 相关,并且可以有若干个实体 B 与一个 A 相关。
一对多关系最为常见。电话号码簿模型显示了一对多和多对多关系。
图: name 与 address 之间的关系
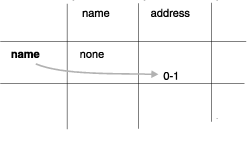
问问您自己:有多少个地址可以与一个名称相关联。您决定一个地址可以与多个名称相关联。例如:您可以了解到多个人在一间公司工作或两个以上的人的住所在同一地址。
图: address 与 name 之间的关系

如果您决定除非地址与至少一个名称相关联否则不能存在,那么写下 1-n 而不是 0-n。
当在任何一端将关系的基数限制为 1 时,就是 1:n 关系。在这种情况下,名称与地址之间的关系是 1:n 关系。
图: number 与 name 之间的关系
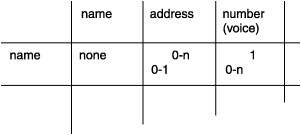
- 一个名称可以与多个传真号码相关联;例如:一间公司可以有若干台传真机。反过来,一个传真号码可以与多个名称相关联;例如:若干个人员可以使用同一个传真号码。
- 调制解调器号码必须刚好与一个名称相关联。(这是为了使示例复杂化而作的任意规定;请将其作为一项设计需求予以接受。)然而,一个名称可以有多个相关联的调制解调器号码;例如:一台公司计算机可以带有若干拨号线路。
- 尽管现实世界中的语音电话号码与地址之间、调制解调器号码与地址之间以及传真号码与地址之间存在某种关系,但这些关系都不必记录在此模型中。通过 name,已存在间接的关系。
图: 已完成的电话号码簿矩阵
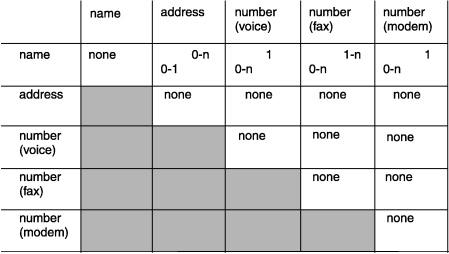
矩阵显示的其他决定包括传真号码与调制解调器号码之间、语音电话号码与传真号码之间或语音电话号码与调制解调器号码之间不存在任何关系。
您可能会不赞同其中某些决定(例如:不支持语音电话号码与调制解调器号码之间的关系)。但是,为了实现本示例,这些就是我们的商业规则。